1. 序列中的所有数都是不大于 k的正整数;
2. 序列中至少有两个数。
3. 序列中的数两两不相等;
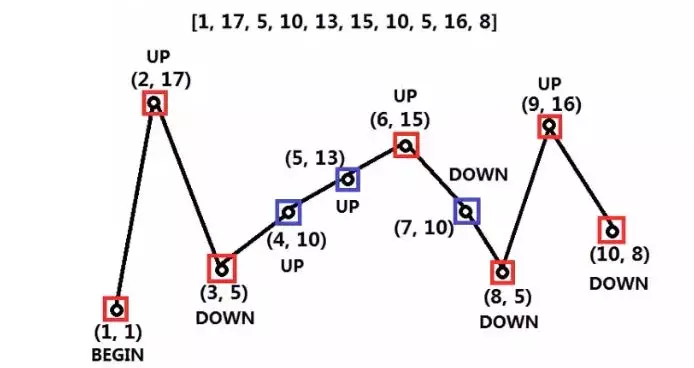
4. 如果第 i – 1个数比第 i – 2个数大,则第 i个数比第 i – 2个数小;如果第 i – 1个数比第 i – 2个数小,则第 i个数比第 i – 2个数大。
比如,当 k = 3时,有下面几个这样的序列:
1 2
1 3
2 1
2 1 3
2 3
2 3 1
3 1
3 2
一共有8种,给定 k,请求出满足上面要求的序列的个数。
/*
dfs深搜+枚举判断
每一个数据可以多次使用,所以需要回溯。先用DFS深搜将可能的结果找出来,然后用if条件进行判断
当只有两个数的时候一定成立,直接加一就可以否则就要满足 :(data[t-2]-data[t-3])*(data[t-1]-data[t-3])<0
现在解释一下,为什么不需要从头开始将条件判断过来,只需要判断刚刚放进去的数能不能满足就可以。
当既不满足t==2又不满足 (data[t-2]-data[t-3])*(data[t-1]-data[t-3])<0条件时,我们直接返回了,没有进行下面的运算,
前面的不满足后面无论满足与否都不需要考虑。
接下来再解释一下为什么不需要判断t的值和n的值得关系。
当t=n+1;时,我们判断的还是前n个数,进入循环以后会发现所有的数都被标记了,没有可以使用的数,会被直接return回去
*/
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int sum,n;
int data[1000]={0},book[1000]={0};
void bfs(int t){
if(t>1){
if(t==2){
sum++;
}
else if((data[t-2]-data[t-3])*(data[t-1]-data[t-3])<0){//数组下标是从0开始的,所以要多减去一个1
sum++;
}
else return ;
}
for(int i = 1;i <= n;i++){
if(book[i]==0){
data[t] = i;//标记
book[i] = 1;//标记
bfs(t+1);
book[i] = 0;//回溯
}
}
return ;
}
int main(){
sum=0;
scanf("%d",&n);
bfs(0);
printf("%d\n",sum);
return 0;
}
仔细观察之后可以看出是一道规律题
首先,如果是1的话构不成摆动序列,而对于2来说是任意组成的符合条件的两个数都是构成摆动序列,
顺序问题是Cn2*2,对于3来说是从中选取三个数,第一个数确定以后,后面的可大可小两种情况,
对于奇数,第一个数一定是中间那个数,第二个数可以大,可以小,使后面的确定下来,
对于偶数来说,第一个数和第二个数一定是中间的两个数,这样就确定了整体的排列顺序,
即从n个数中选择2到n个数的总和*2即为答案,然后C(N,1)+C(n.2)+。。。+C(n,n)=2的n次方-1。
*/#include <stdio.h>
#include <math.h>
int main()
{
int k;
scanf(“%d”, &k);
printf(“%d”, (int)(pow(2, k) – k – 1) * 2);
return 0;
}
使用动态规划的第一步就是将表建立起来
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 2 | 2 | ||||||
| 3 | 6 | 2 | |||||
| 4 | 12 | 8 | 2 | ||||
| 5 | 20 | 20 | 10 | 2 | |||
| 6 | 30 | 40 | 30 | 12 | 2 | ||
| 7 | 42 | 70 | 70 | 42 | 14 | 2 | |
| 8 | 56 | 112 | 140 | 112 | 56 | 16 | 2 |
仔细观察可以发现:
/*
题目有点排列组合的意思,那么我们可以考虑能否使用动态规划来解决,
使用动态规划的第一步就是将表建立起来
*/
#include<iostream>
using namespace std;
int main()
{
int k;
int a[21][21];
long sum = 0;
cin>>k;
for(int i = 2; i <= k; i++){
a[i][i] = 2;
a[i][2] = i*(i-1);
for(int j = 3; j < i; j++){
a[i][j] = a[i-1][j]+a[i-1][j-1];
}
}
for(int i = 2; i <= k; i++){
sum += a[k][i];
}
cout<<sum;
return 0;
}

